بحث عن المصفوفات يجب العلم أن المصفوفة هي عبارة عن شكل مستطيلي يتكون مِن أرقام أو عبارات أو حتي رموز و يُطلق عليهذه المحتويات إسم العناصر أو الإدخالات و جميعها مُرتب في أعمدة و صفوف و تنقسم هذه العناصر أو المحتويات إلي قسمين إثنين الأول هو العناصر الحقيقية والآخر هو العناصر المعقدة ومِن الجدير بالذكر أن المصفوفة قد تحتوي علي أرقام حقيقية أو أرقام مركبة ، و للمصفوفة تاريخ عريق للغاية في حل المعادلات الخطية وهي معروفة باسم صفائف مِنذ عام 1800 ميلادياً و منذاك الحين انتشرت إلي دول العالم أجمع عن طريق العلماء .

بحث عن المصفوفات و حجمها
حجم أي مصفوفة يعتمد علي عدد الأعمدة و الصفوف التي تحتويها و في الغالب يُرمز للمصفوفة ب( م ن ) بينما أعمدة المصفوفة يُرمز لها ب( و م × ن ) أو ( م ن- by ) ، أما أبعاد المصفوفة فيُرمز لها ( م و ن ) .
المصفوفة التي تحتوي علي صف واحد فقط لا أكثر تُعرف بإسم نواقل التوالي بينما المصفوفة التي تحتوي علي عمود واحد فقط تُعرف بإسم ناقلات العود أما المصفوفة التي عدد صفوفها و عدد أعمدتها واحد فإنها تُعرف بإسم المربعة و المصفوفة التي ليس لها عدد معين مِن الصفوف أو الأعمدة فهي معروفة بإسم اللانهائية و المصفوفة التي لا تحتوي علي أعمدة أو صفوف فإنها تُعرف بإسم المصفوفة الفارغة .

الجوانب الحسابية للمصفوفات
حسابات المصفوفات تقوم غالباً علي تقنيات كثيرة مختلفة و متنوعة فللمصفوفات المقدرة علي حل الكثير مِن المشاكل عبر طريقتي الخوارزميات بالشكل المباشر أو النهج المتكرر فمثلاً عن طريق المتجهات الذاتية للمصفوفة المربعة يُمكن إيجاد تسلسل الناقلات إذا ما تقاربت للمتجه الذاتي عندما تميل قيم الصفوف فيها إلي ما لا نهاية .
لكي تستطيع أن تختار خوارزمية مناسبة لحل مشكلة ما فيجب و لابد أن أن تحدد كلاً مِن فعالية و دقة كافة الخوارزميات المتاحة و نطاق دراسة هذه المسائل يُطلق عليه إسم المسائل العددية للجبر الخطي و هو مثال للكثير مِن الحالات العددية الأخري فلكلاً منها و تحديد مدي تعقيد الخوارزمية يعني وجود الحدود العليا أو علي الأقل تقديرات عدد العمليات الأولي كالضرب و الإضافات .
بحث عن المصفوفاتالتطبيقات علي المصفوفات
للمصفوفات الكثير و الكثير مِن التطبيقات المختلفة سواء في الرياضيات أو حتي في العلوم حيث يُمكن الإستفادة مِن المصفوفات بشكل كبير للغاية في تمثيل مضغوط لمجموعة مِن الأرقام بالمصفوفة عن طريقالإعتماد علي مجموعة بدائل لأية عملية تحتاج لحسابات معقدة و لهذا الأمر الكثير مِن النظريات التي أبرزها :
1- الإحصاء و الإحتمالات
يُمكن تطبيق هذه النظرية علي المصفوفات العشوائية و المصفوفات المربعة عن طريق ناقلات الإحتمالات و يتم هذا عن طريق إدخالا غير قابلة للسلبية .
2- التماثلات و التحويلات
هذه النظرية تلعب دور كبير للغاية بل و رئيسي في الفيزياء الحديثة و بشكل خاص في مجال الجسيمات .
3- الرسم البياني
4- التركيبات الخطية
5- التحليل و الهندسة
6- البصريات الهندسية
7- الإلكترونيات
جمع المصفوفات
قد يهمك
يُمكن الجمع بين مصفوفتين إذا ما كانا مِن نفس القياس و حاصل جمع المصفوفتين يُعرف بكونه المصفوفة الناتجة مِن جمع كافة العناصر المتناظرة في مصفوفتين .
ضرب المصفوفات
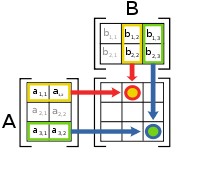
ضرب المصفوفات هو عبارة عن ضرب العنصر الوحيد مِن كل عنصر مِن عناصر المصفوف و النتيجة تكون مصفوفة جديدة تماماً تحتوي علي نفس عدد العناصر
