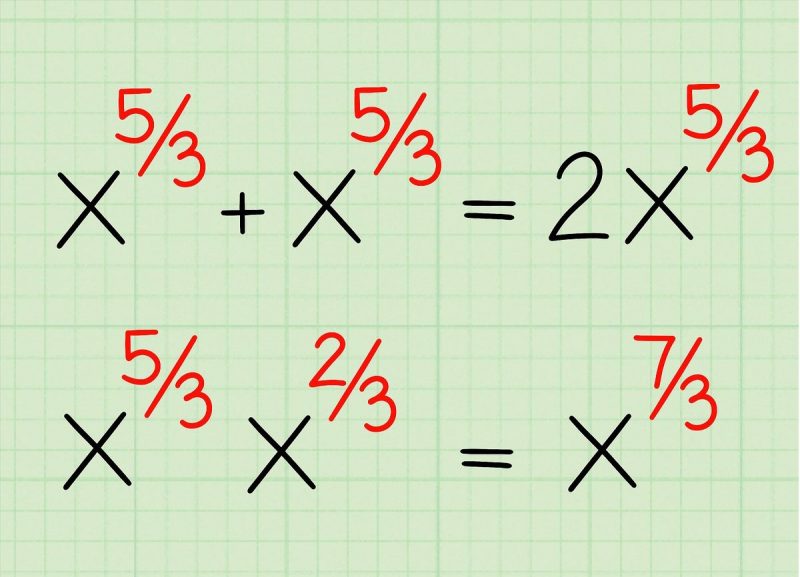بحث عن الاسس النسبية في الرياضيات ، والتي كانت أول من كتبها في الرياضيات هو العالم مايكل ستيفل ، وكانت الأرقام بقاعدة أو أساس من اثنين ، ومن خلال ما قدمه بحث عن الاسس النسبية في الرياضيات ، وجد أن الهدف من ذلك كان استخدام الاسس في تخفيض ، أو التقليل من عدد منازل الرقم ، وهذا لأن كثرة الأرقام كانت تؤدي لضياع عدد منهم ، والوقوع في الأخطاء ، وكانت المسألة الرياضية معقدة بسبب ذلك.
بحث عن الاسس النسبية في الرياضيات بالتفصيل
ما هي الاسس النسبية

اقرأ أيضا
الاسس النسبية تختلف بشكل كامل على الاسس العادية في الرياضيات ، حيث أن العدد النسبي هو ما يمكن كتابته على شكل بسط ومقام ، وعليه يكون الأس النسبي هو ما يكتب على شكل بسط ومقام ، أما الأسس العادية فيكون الأس فيها رقم واحد فقط موجبا أو سالبا أو حتى صفر ، كما أن الأسس النسبية تعامل معاملة الأسس العادية تماما ، ويتم تطبيق قوانين الاسس العامة عليها.
القاعدة الأولى الجذور التربيعية والتكعيبية في الأسس النسبية

اقرأ أيضا
تعبر الأسس النسبية عن قيمة الجذر التربيعي والجذر التكعيبي ، أي أنه بدلا من كتابة العدد بإشارة الجذر ، يتم كتابته شكل أس له بسط رقم واحد ، والمقام الرقم اثنان للجذر التربيعي ، وثلاثة تكون للجذر التكعيبي ، ومثال للتوضيح:
– في حالة كان العدد زوجي موجب ، وكانت س عددا حقيقيا موجبا ، مثل الجذر التربيعي فإن س√ = س1/2
– وفي حالة كان العدد فرديا موجبا ، وكانت س هي العدد الحقيقي الموجب ، مثل الجذر التكعيبي فإن س∛ = س1/3
القاعدة الثانية عمليتي الجمع والطرح في الأسس النسبية

اقرأ أيضا
الأسس النسبية ليست عبارة عن جذور ، حيث أن هناك الأسس النسبية التي يكون بها الأس عبارة عن كسر له بسط مخالف للرقم واحد ، فيجب الرجوع إلى قوانين الجمع والطرح في الكسور ، والتي تكون بحاجة إلى توحيد المقامات في حالة كانت مختلفة في قيمة المقام بين الكسرين ، وذلك قبل أن يتم القيام بعملية الجمع ، أو الطرح لها ، ومثال للتوضيح:
– مثال على عملية الجمع س1/4 * س1/2 = س( 1/4+1/2) = س(2/4+1/4) = س3/4
– مثال على عملية الطرح س1/2 / س1/3 = س(1/2-1/3) = س(3/6-2/6) = س1/6
القاعدة الثالثة عمليتي القسمة والضرب في الأسس النسبية
وهنا نوضح ماذا لو أن الأساس هو المختلف بينما الأسس ، هي التي تكون متشابهة ، فلا بد من اجراء عمل لتوزيع الأس على العددين المضروبين ، أو المقسومين وإيجاد ناتج الأس منهما ، وهو الحل السريع في تلك الحالة ، ومن ثم يتم اجراء عملية الضرب أو القسمة ، ومثال للتوضيح :
– مثال على عملية الضرب (س*ص)5 = س5 * ص5.
– مثال على عملية القسمة (س/ص)5 = س5 / ص5.
القاعدة الرابعة الأسس النسبية السالبة
في حالة كانت الأسس النسبية السالبة ، والتي تنتج عندما يكون الرقم فيها الأس في المقام ، يمكن أن يتم رفع الرقم في البسط مع وضع الإشارة للأس بالسالب ، والتعامل مع الأس بعد ذلك في عمليات الجمع ، أو الطرح أو القسمة أو الضرب بالطريقة المعتادة في القواعد السابقة ، ومثال على ذلك:
– 1 / س1/2 = س-1/2 وهكذا الحال في كل العمليات الأولية الحسابية للأسس.