مساحة متوازي الاضلاع هو عبارة عن شكل أو مضلع رباعى فيه كل ضلعين متقابلين متوازيين ومتساويين وكل زاويتين به متقابلتين متساويتين فى القياس والقطران حيث ينصف كل نهم الأخر ومجموع قياسات زواياه تبلغ 360 درجة . تعالو بنا فى هذا المقال نعرف المزيد عن متوازى الأضلاع وحساب مساحته ومحيطه
تعرف على
سوف نتعرف معا فى هذا المقال على مساحة متوازي الاضلاع
خصائص متوازى الأضلاع
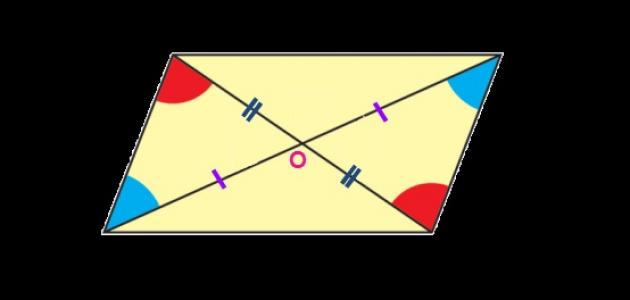
- كل ضلعين بمتوازى الاضلاع متقابلين متوازيين ومتساويين فى الطول
- بالنسبة لقطران متوزاى الأضلاع ينصف كل منهما الأخر
- القطران به يتقاطعان فى نقطة تمثل مركز تماثل لمتوازى الأضلاع والتى يطلق عليها مركز متوازى الأضلاع
- كل زاويتين به متقابلتين متساويتين فى القياس
- كل زاويتين متتاليتين متكاملتين ويصل مجموع قياسهم إلى 180 درجة
- مساحة متوازى الأضلاع تساوى ضعف مساحة المثلث الذى يتم تشكيله بضلعين من أضلاع متوازى الأضلاع وقطر من أقطاره
- مجموع مربعات أطوال الأضلاع يساوى مجموع مربعى قطرى متوازى الأضلاع
حالات خاصة عن متوازى الأضلاع
- فى حالة تعامد قطرى متوازى الأضلاع وكتن طولا كل ضلعين متجاورين متساويين أصبح هذا المتوازى مربع
- أما فى حالة إذا تساوى قطرى متوازى الأضلاع وكانت إحدى زواياه قائمة كان هذا الشكل مستطيل
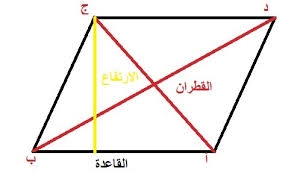
حساب مساحة متوازي الاضلاع بدلالة مساحة المثلث
مساحة متوازى الأضلاع = مجموع مساحة المثلثين ومساحة المثلث = 0.5 × القاعدة × الإرتفاع
لذا فإن مساحة متوازى الأضلاع = طول القاعدة × الإرتفاع= 2 × ( 0.5 × طول القاعدة × الإرتفاع)
كما تساوى ايضا : 2× ( 0.5 × طول الضلع الأول × طول الضلع الثانى × جيب الزاوية المحصورة بينهما )
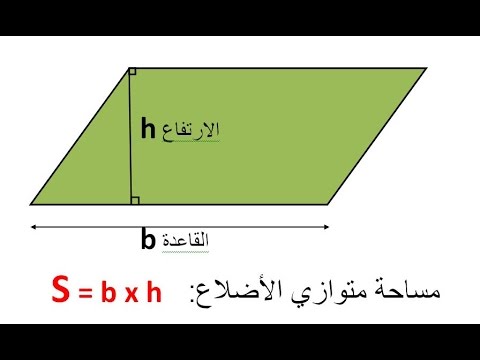
كيفية حساب مساحة متوازى الأضلاع
متوازى الأضلاع هو عبارة عن شكل ثنائى الأبعاد يمكن حساب مساحته ومحيطه بسهولة . ولمعرفة قانون حساب مساحته ومحيطه قام العلماء بتجزئة المتوازى لمثلث ومستطيل ووجدوا قانون لحساب مساحته والذى يتمثل فى :
مساحة متوازى الأضلاع = طول القاعدة × الإرتفاع
مثال على ذلك :
قم بحساب مساحة متوازى الأضلاع الذى يبلغ طول أحد أضلاعه 5 سم وإرتفاعه 4 سم ؟
الحل :
مساحة متوازى الأضلاع = طول القاعدة × الإرتفاع
مساحة متوازى الأضلاع = 5×4 = 20 سم2
مثال أخر
متوازى أضلاع طول كل ضلعين متتاليين 6سم و8 سم وإرتفاعه المناظر للضلع الأكبر 12 سم ، قم بحساب الإرتفاع المناظر للضلع الأصغر
الحل :
مساحة متوازى الأضلاع = طول القاعدة × الإرتفاع
مساحة متوازى الأضلاع = 8 × 12=96سم2
الإرتفاع المناظر للضلع الأصغر = المساحة /القاعدة الصغرى
الإرتفاع المناظر للضلع الأصغر = 96 /6 = 16 سم2
حساب محيط متوازى الأضلاع
يعد محيط أى مضلع من المضلعات يساوى مجموع أطوال أضلاعه وسوف نعرف ذلك من خلال عرض هذا المثال :
مثال
قم بحساب محيط متوازى الأاضلاع الذى يبلغ طول أحد أضلاعه 15 والضلع الأخر 20 متر ؟
الحل:
محيط متوازى الأضلاع = 2(طول الضلع الأكبر + طول الضلع الأصغر )
محيط متوازى الأضلاع = 2 × ( 15 + 20 ) = 2× 35= 70 سم
مثال أخر
ملعب كرة على شكل متوازى الأاضلاع يبلغ محيطه حوالى 80 متر وطول أحد أضلاعه 15 متر أوجد طول الضلع الأخر
الحل :
طول الضلع الثانى = محيط متوازى الأضلاع – ( 2× طول الضلع ) /2
طول الضلع الثانى = 80 – ( × 15) / 2 = 25 متر
متوازى الأضلاع هو عبارة عن شكل رباعى هندسي منتظم كل ضلعين متقابلين به متوازيين ومتساويين فى الطول ، وكل زاويتين متقابلتين متساويتين وقطراه ينصفات بعضهما البعض ، كما أن مجموع قياس زواياه حوالى ثلاثمائه وستين درجة وهو شبيه بالمعين. ولقد تعرفنا فى هذا المقال على أهم خصائص متوازى الأضلاع فضلا عن كيفية حساب مساحة متوازي الاضلاع ومحيطه ، كما اشرنا لذلك بمجموعه من الأمثلة